What is Wasserstein Distance in Machine Learning?

Wasserstein Distance

Wasserstein distance -- also known as Earth Mover’s Distance -- measures the distance between two probability distributions over a given region. Wasserstein distance is helpful for statistics on non-overlapping numerical distribution moves and higher dimensional spaces (images, for example). Wasserstein distance is a fairly old calculation -- it was formulated in 1781. In the case of a one-dimensional distribution, it captures how much the shape and distance to the mean of a distribution is retained in moving one distribution to the other.

Example

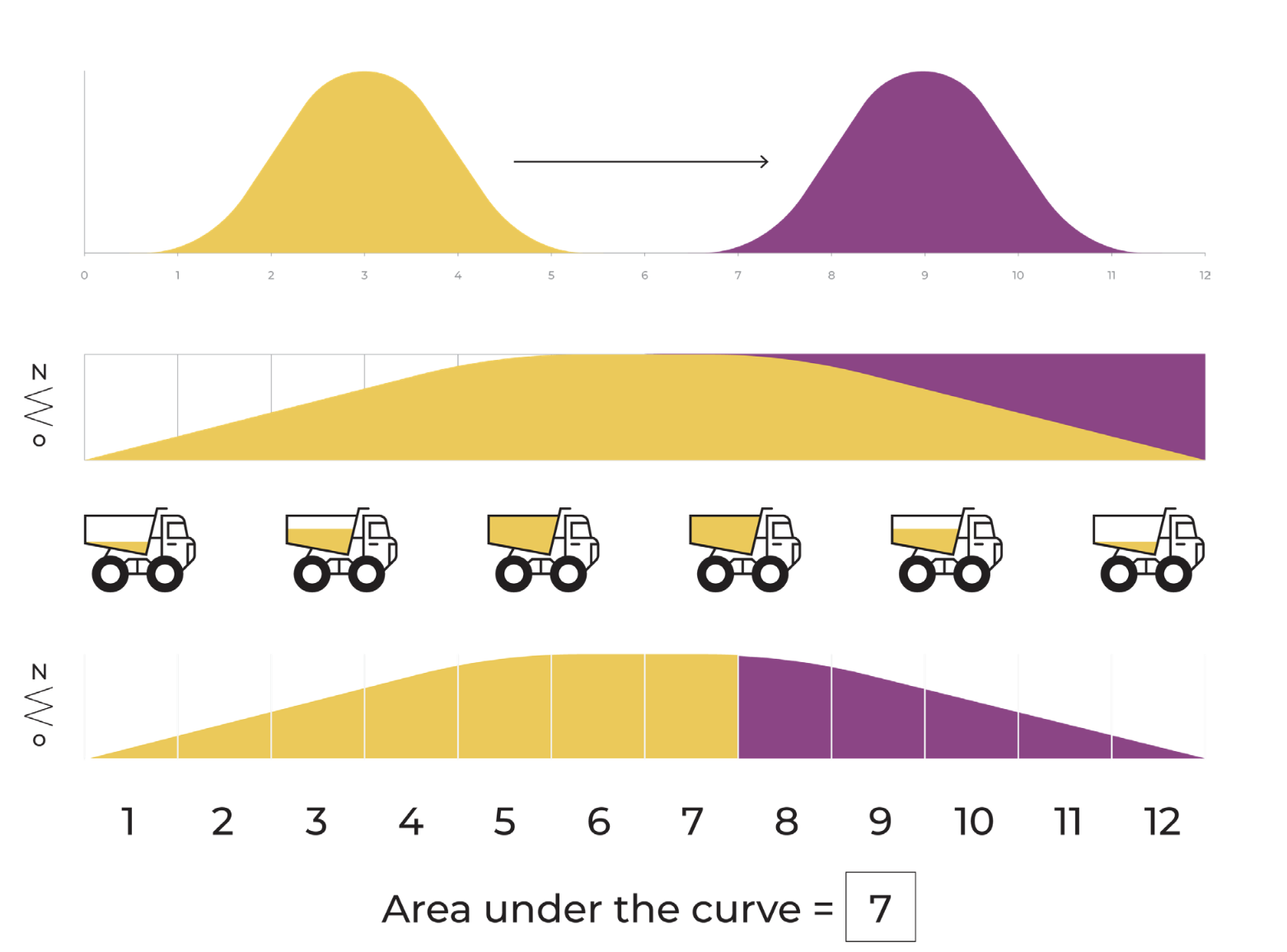
The Wasserstein distance or Earth Mover’s Distance can be simply demonstrated using a one-dimensional case such as that which is illustrated in the image (originally the EMD algorithm was designed to solve a problem around moving dirt). The distance here can be thought of as the work needed to move one pile of dirt into another pile of dirt. The dirt is filled up by a truck along a straight road (the X-axis) by putting the dirt into the truck. The work needed to move the dirt is calculated by each unit along the X-axis, as well as how much dirt is in the truck, and how many units of dirt that the truck can transport. The truck empties the dirt into the other distribution. The further away the means of the distributions, the larger the distance because the truck will transport the dirt farther to get from one mean to the other. The more spread out and overlapping the distributions are, the smaller the number. Compared to KL divergence, EMD handles naturally non-overlapping distributions where KL/PSI need modifications.