JS Div(P, Q) = ½ KL-DIV(P,M) + ½ KL-DIV(Q,M)
Reference = M (mixture distribution) = ½ (P + Q)
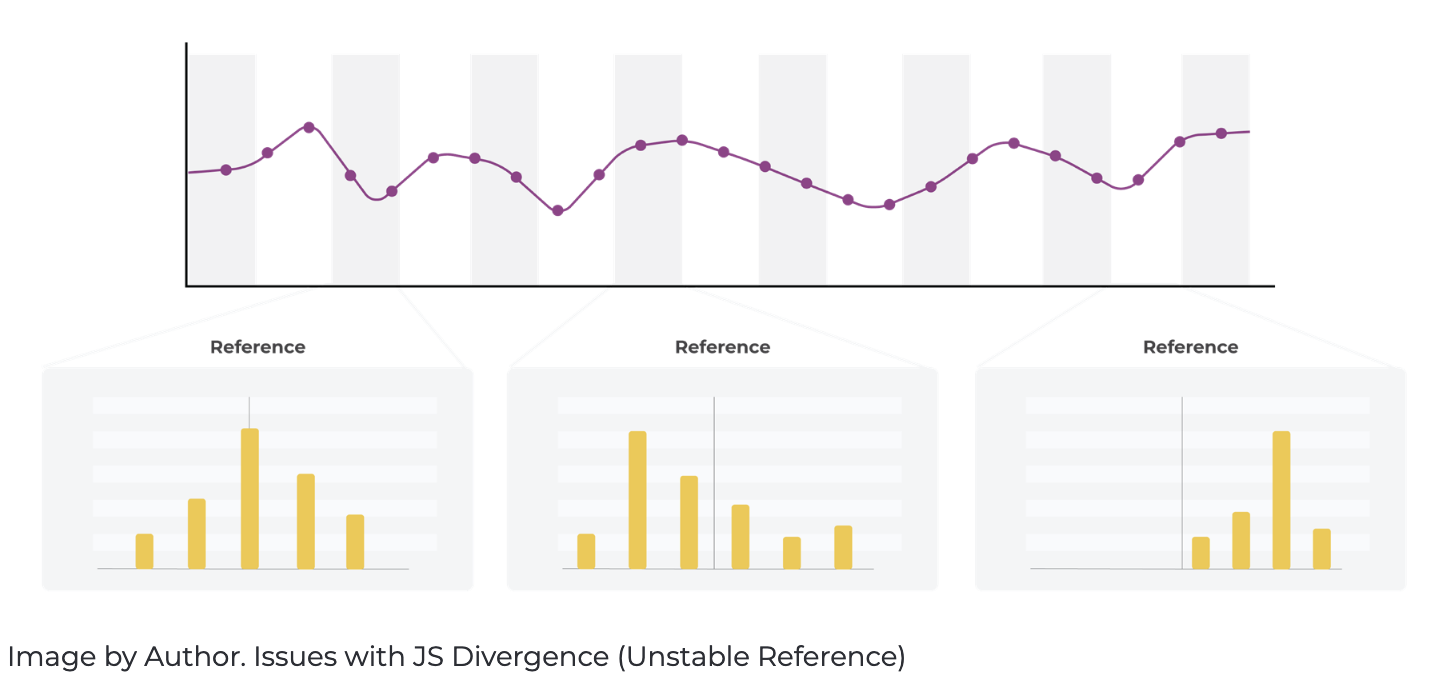
JS Divergence has some useful properties. Firstly, it’s always finite, so there are no divide-by-zero issues. Divide by zero issues come about when one distribution has values in regions the other does not. Secondly, unlike KL-Divergence, it is symmetric. The JS divergence uses a mixture of the two distributions as the reference. There are challenges with this approach for moving window checks; the mixture-reference changes based on the changes in the moving window distribution. Since the moving window is changing each period, the mixture- reference is changing, and the absolute value of the metric in each period can not be directly compared to the previous periods without thoughtful handling. There are workarounds but not as ideal for moving windows.
The moving window changes each period for every distribution check. It represents a sample of the current periods distribution. The JS Distribution
has a unique issue with a moving window, in that the mixture will change with each window of time you are comparing. This causes the meaning of the value returned by JS Divergence to shift on a periodic basis, making comparing different time frames on a different basis, which is not what you want. The PSI and JS are both symmetric and have potential to be used for metric monitoring. There are adjustments to PSI that we recommend versus JS as a distance measure for moving windows used for alerts.