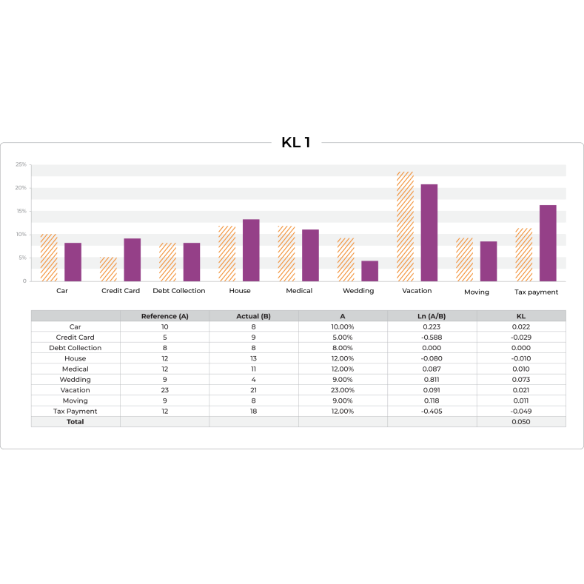
The Kullback-Leibler Divergence metric is calculated as the difference between one probability distribution from a reference probability distribution. KL divergence is sometimes referred to as ‘relative entropy’ and best used when one distribution is much smaller in sample and has a large variance.
Equation:
KLdiv = Ea[ln(Pa/Pb)] = ∑ (Pa)ln(Pa/Pb)
KL Divergence is a well-known metric that can be thought of as the relative entropy between a sample distribution and a reference (prior) distribution.
Like PSI, KL Divergence is also useful in catching changes between distributions. Also similar to PSI, it has its basis in information theory. One important difference from PSI is that KL Divergence is not symmetric. A reversed distribution will have a different value – you will get different values
going from A -> B then B -> A. There are a number of reasons that having a non-symmetric metric is not ideal for distribution monitoring in that you get different values, when you switch what is the reference versus compared distribution. This can come across as non-intuitive to users of monitoring.