KL Divergence: When To Use Kullback-Leibler divergence
The basics of KL divergence and how it is used in drift monitoring
What Is KL Divergence?
Kullback-Leibler divergence metric is a statistical measure from information theory that quantifies the difference between one probability distribution from a reference probability distribution. KL divergence is also known as relative entropy.
This post covers:
- How to use KL divergence in machine learning (ML);
- How KL divergence works in practice; and
- When KL divergence should and shouldn’t be used to monitor for drift.
KL Divergence Formula
KL divergence is a non-symmetric metric that measures the relative entropy or difference in information represented by two distributions. It can be thought of as measuring the distance between two data distributions showing how different the two distributions are from each other.
There is both a continuous form of KL divergence
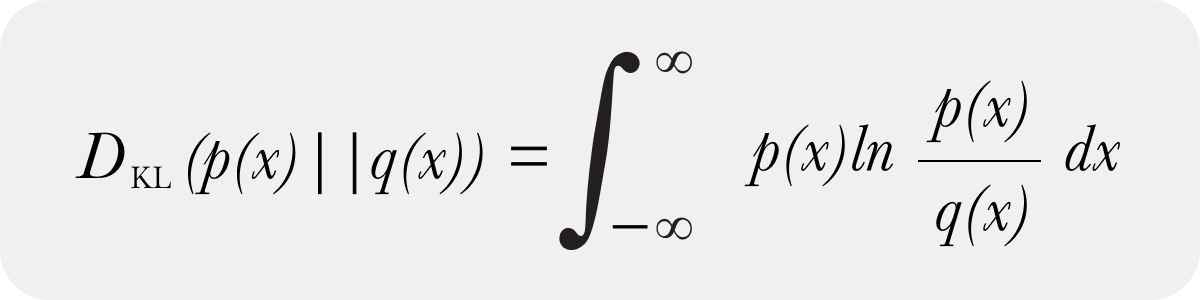
And a discrete form of KL Divergence
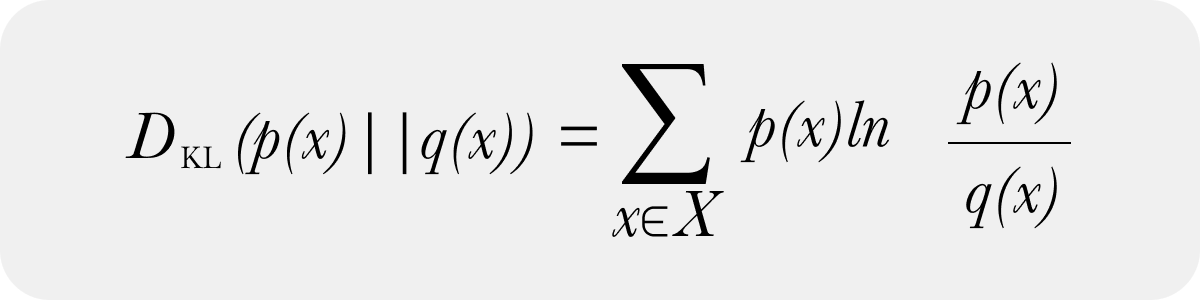
In model monitoring, we almost exclusively use the discrete form of KL divergence and obtain the discrete distributions by binning data. The discrete form of KL divergence and continuous forms do converge as the number of samples and bins limit move to infinity. There are optimal selection approaches to the number of bins to approach the continuous form. In practice, the number of bins can be far less than the above number implies – and how you create those bins to handle the case of 0 sample bins is more important practically speaking than anything else (a future post with code will address how to handle zero bins naturally).
How Is KL Divergence Used in Model Monitoring?
In model monitoring, KL divergence is used to monitor production environments, specifically around feature and prediction data. KL Divergence is utilized to ensure that input or output data in production doesn’t drastically change from a baseline. The baseline can be a production window of data or a training or validation dataset.
Drift monitoring can be especially useful for teams that receive delayed ground truth to compare against production model decisions. These teams can rely on changes in prediction and feature distributions as a proxy for performance.
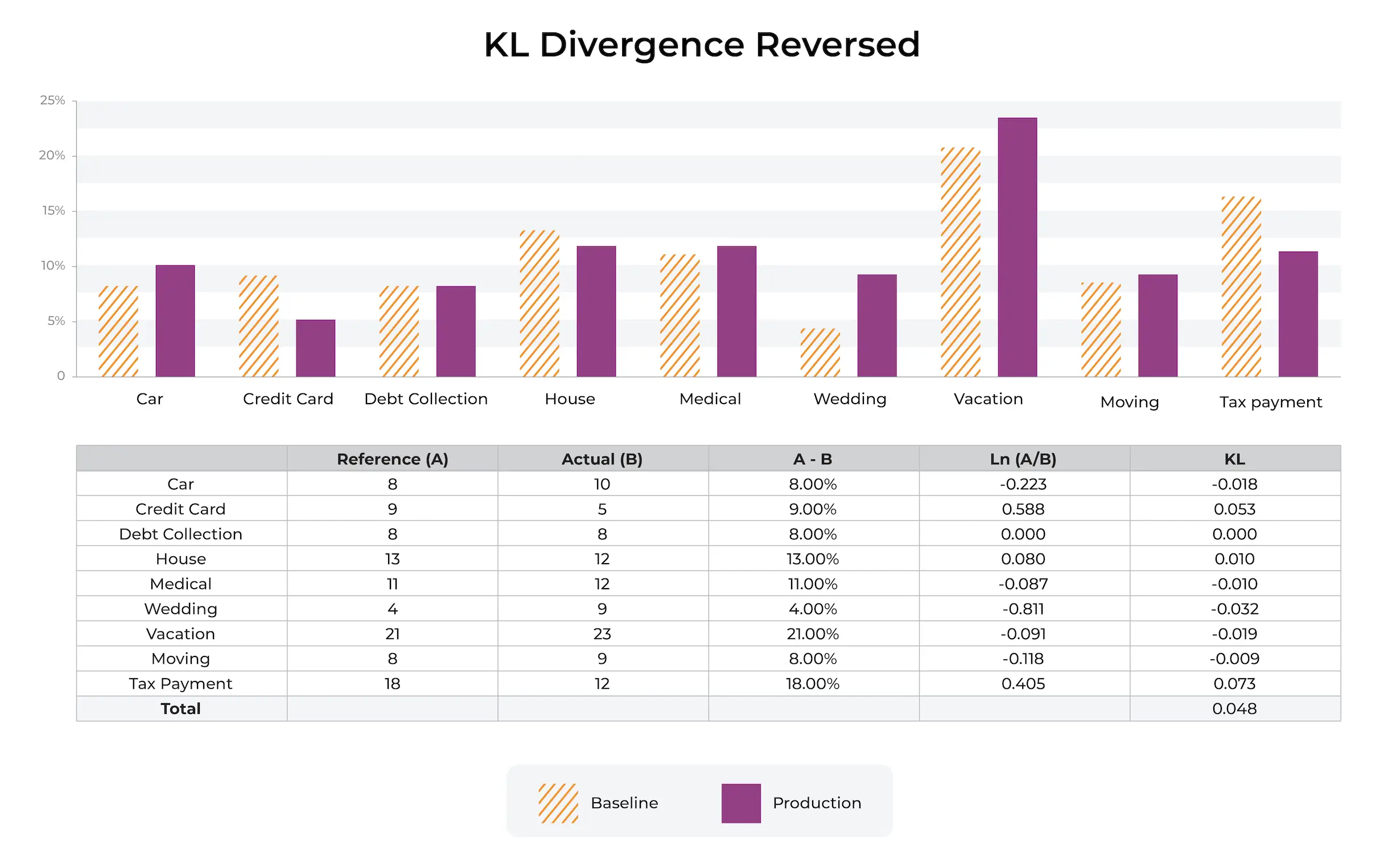
KL divergence is typically applied to each feature independently; it is not designed as a covariant feature measure but rather a metric that shows how each feature has diverged independently from the baseline values.
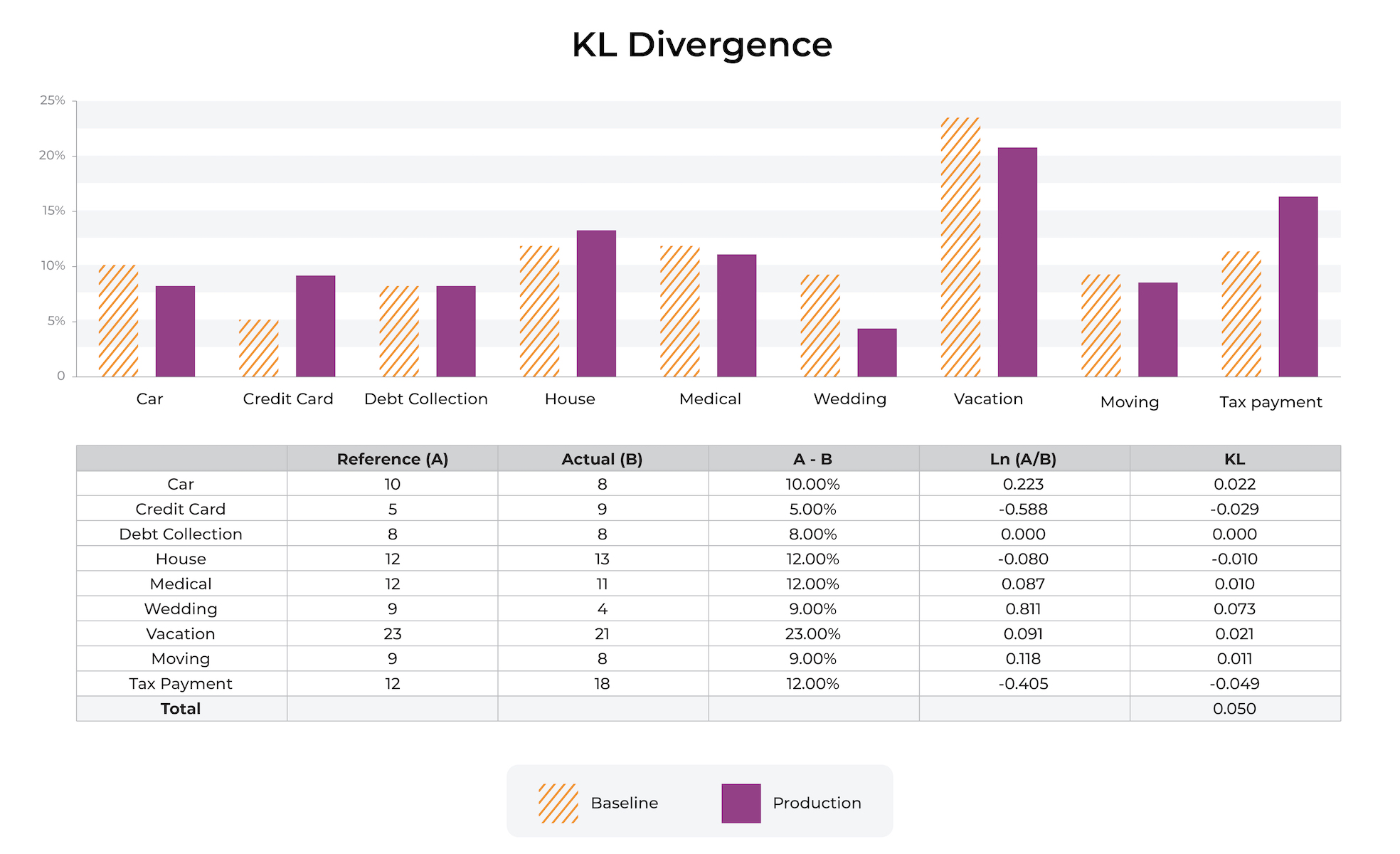
The p(x) shown above in orange stripes is the reference or baseline distribution. The most common baselines are either a trailing window of production data or the training datasets. Each bin additively contributes to KL divergence. The bins jointly add up to the total percent distribution.
✏️ NOTE: sometimes non-practitioners have a somewhat overzealous goal of perfecting the mathematics of catching data changes. In practice, it’s important to keep in mind that real data changes all the time in production and many models extend well to this modified data. The goal of using drift metrics is to have a solid, stable and strongly useful metric that enables troubleshooting.
Is KL Divergence An Asymmetric Metric?
Yes. If you swap the baseline distribution p(x) and sample distribution q(x), you will get a different number. Being an asymmetric metric has a number of disadvantages as teams use KL divergence for troubleshooting data model comparisons. There are times when teams want to swap out a comparison baseline for a different distribution in a troubleshooting workflow, and having a metric where A / B is different than B / A can make comparing results difficult.
This is one reason that Arize’s model monitoring platform defaults to population stability index (PSI), a symmetric derivation of KL Divergence, as one of the main metrics to use for model monitoring of distributions.
Differences Between Continuous Numeric and Categorical Features
KL divergence can be used to measure differences between numeric distributions and categorical distributions.
Numerics
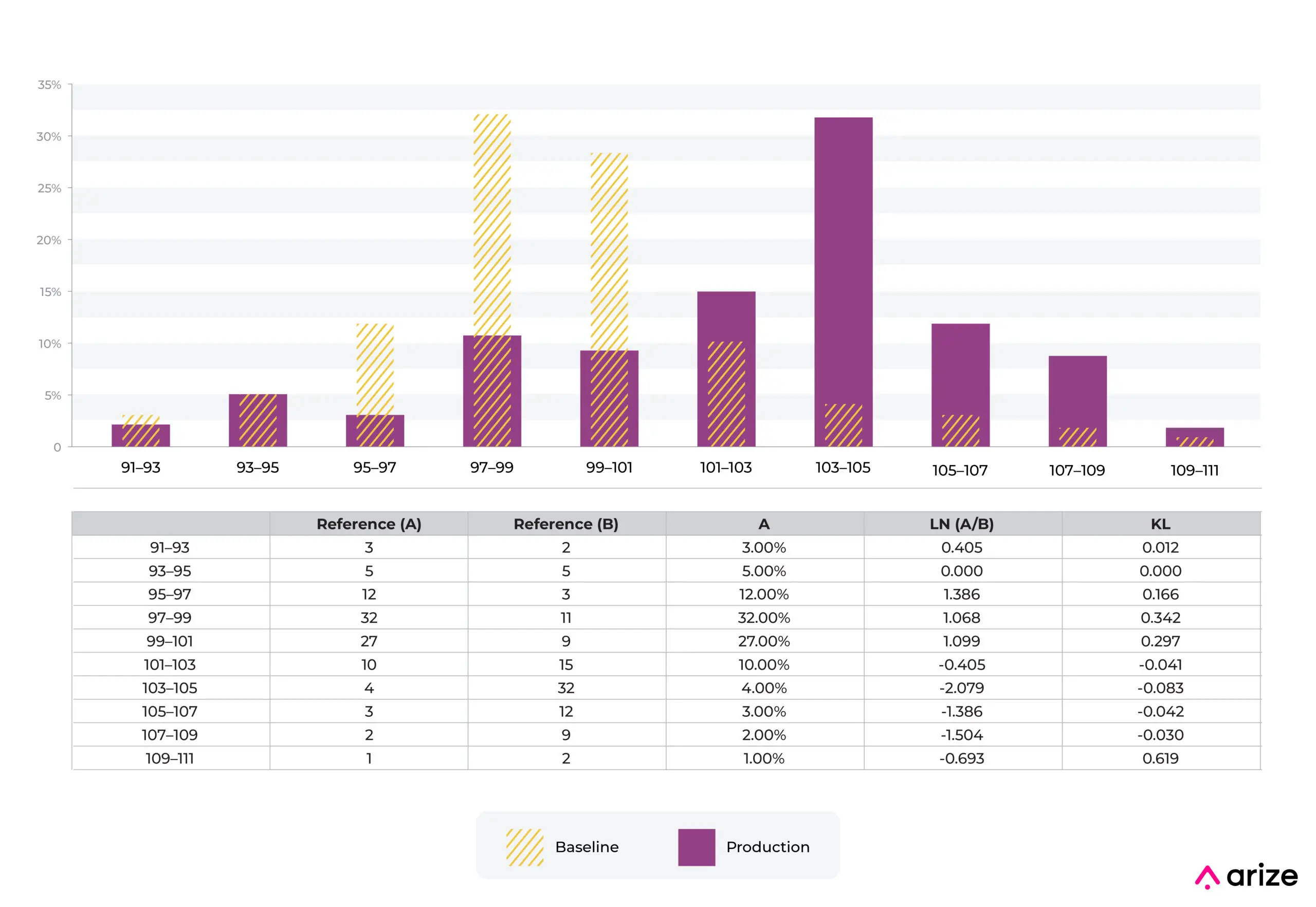
In the case of numeric distributions, the data is split into bins based on cutoff points, bin sizes and bin widths. The binning strategies can be even bins, quintiles and complex mixes of strategies and does affect KL divergence in a big way.
Categorical
The monitoring of KL divergence tracks large distributional shifts in the categorical datasets. In the case of categorical features, often there is a size where the cardinality gets too large for the measure to have much usefulness. The ideal size is around 50-100 unique values – as a distribution has higher cardinality, the question of how different the two distributions are and if it really matters gets muddied.
High Cardinality
In the case of high cardinality feature monitoring, out-of-the-box statistical distances do not generally work well – instead, we typically recommend two options:
- Embeddings: In some high cardinality situations, the values being used – such as User ID or Content ID – are already used to create embeddings internally. Arize embedding monitoring can help.
- Pure High Cardinality Categorical: In other cases, where the model has encoded the inputs to a large space, just monitoring the top 50-100 top items with KL Divergence and all other values as “other” can be useful.
Lastly, sometimes what you want to monitor is something very specific such as the percent of new values or bins in a period. These can be setup more specifically with data quality monitors.
KL Divergence Example
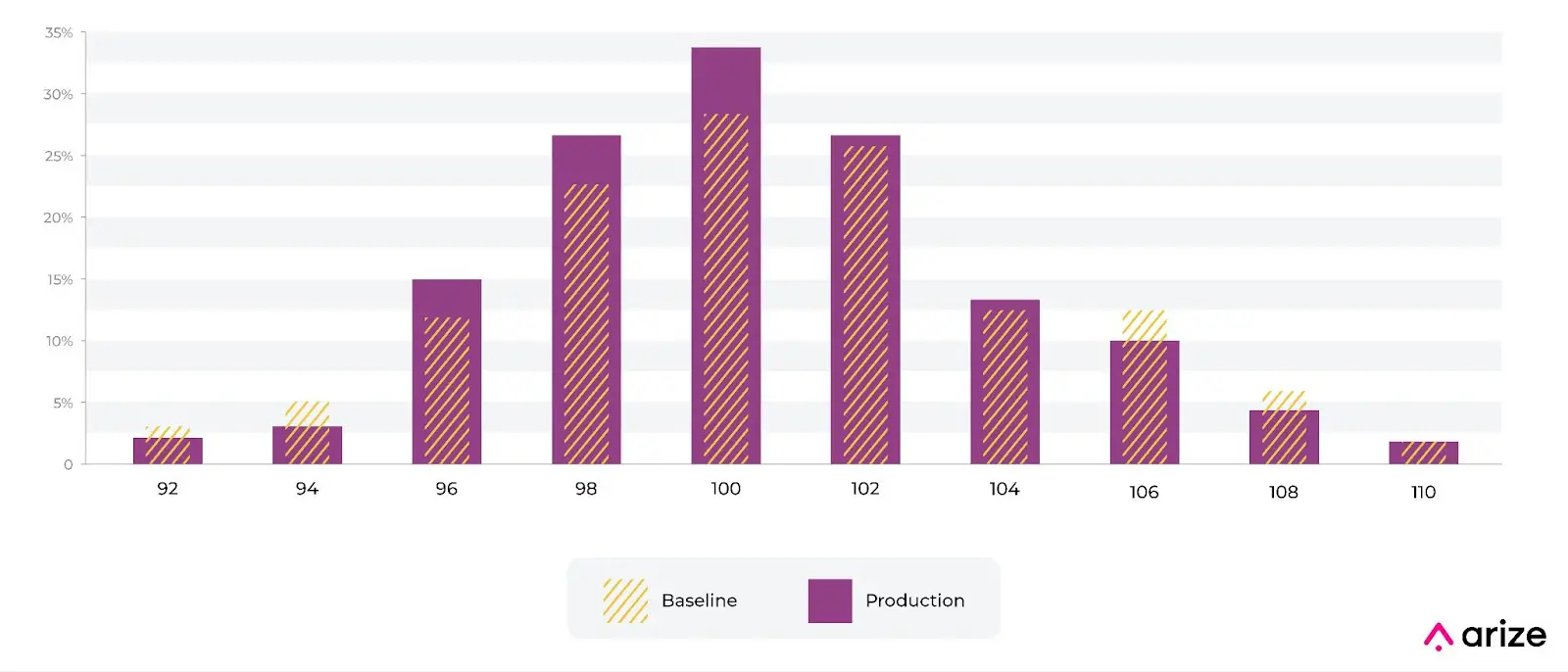
Here is an example. Imagine we have a numeric distribution of charge amounts for a fraud model. The model was built with the baseline shown in the picture below from training. We can see that the distribution of charges has shifted. There are a number of industry standards around thresholds, we actually recommend using a production trailing value to set an auto threshold. There are many examples in production where a fixed setting does not make sense.
Intuition Behind KL Divergence
It’s important to have a bit of intuition around the metric and changes in the metric based on distribution changes.
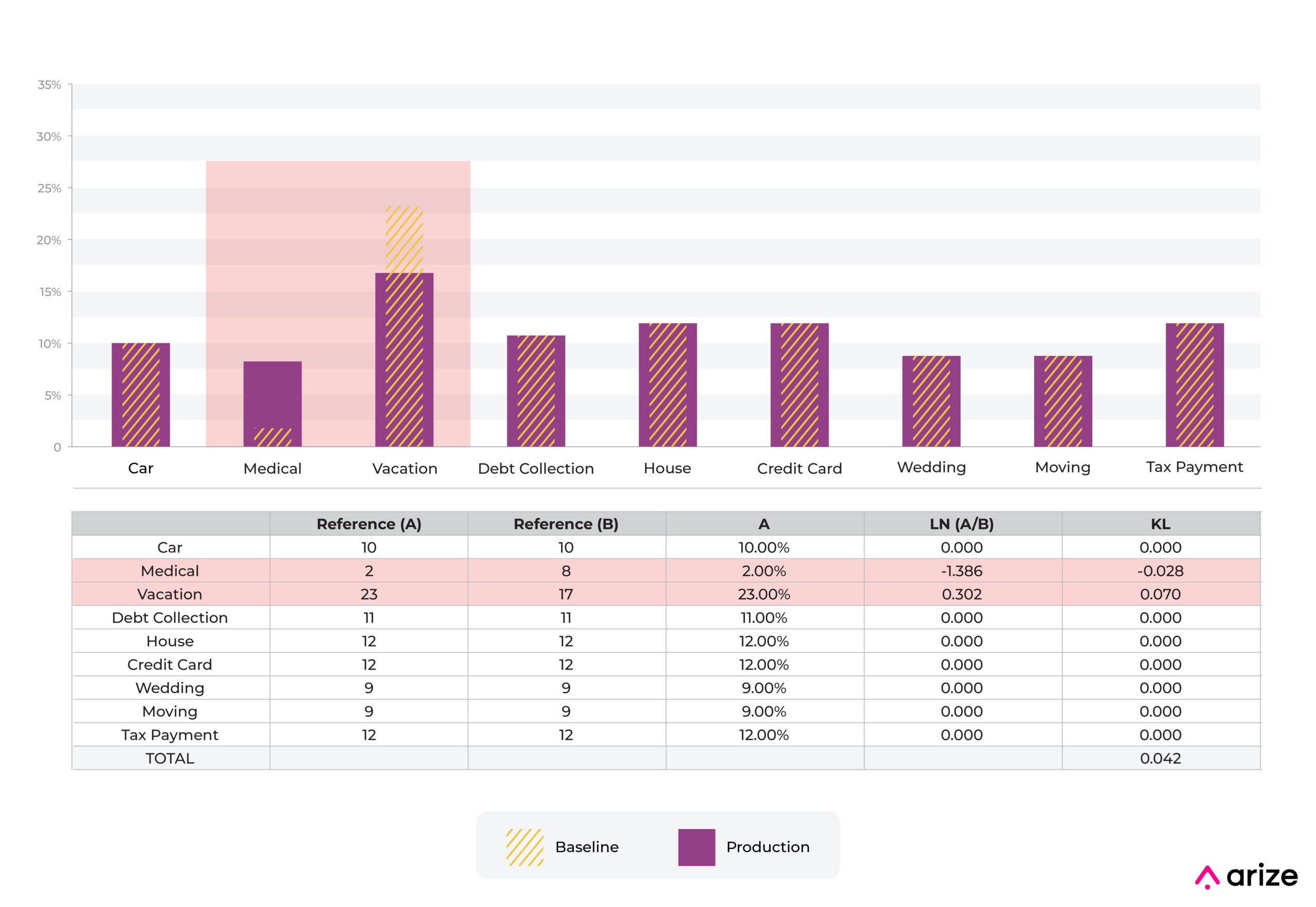
The above example shows a move from one categorical bin to another. The predictions with “medical” as input on a feature (use of loan proceeds) increased from 2% to 8%, while the predictions with “vacation” decreased from 23% to 17%.
In this example, the component to KL divergence related to “medical” is -0.028 and is smaller than the component for the “vacation” percentage movement of 0.070.
In general, movements that decrease the percentage and move it toward 0 will have a larger effect on this statistic relative to increases in the percentage.
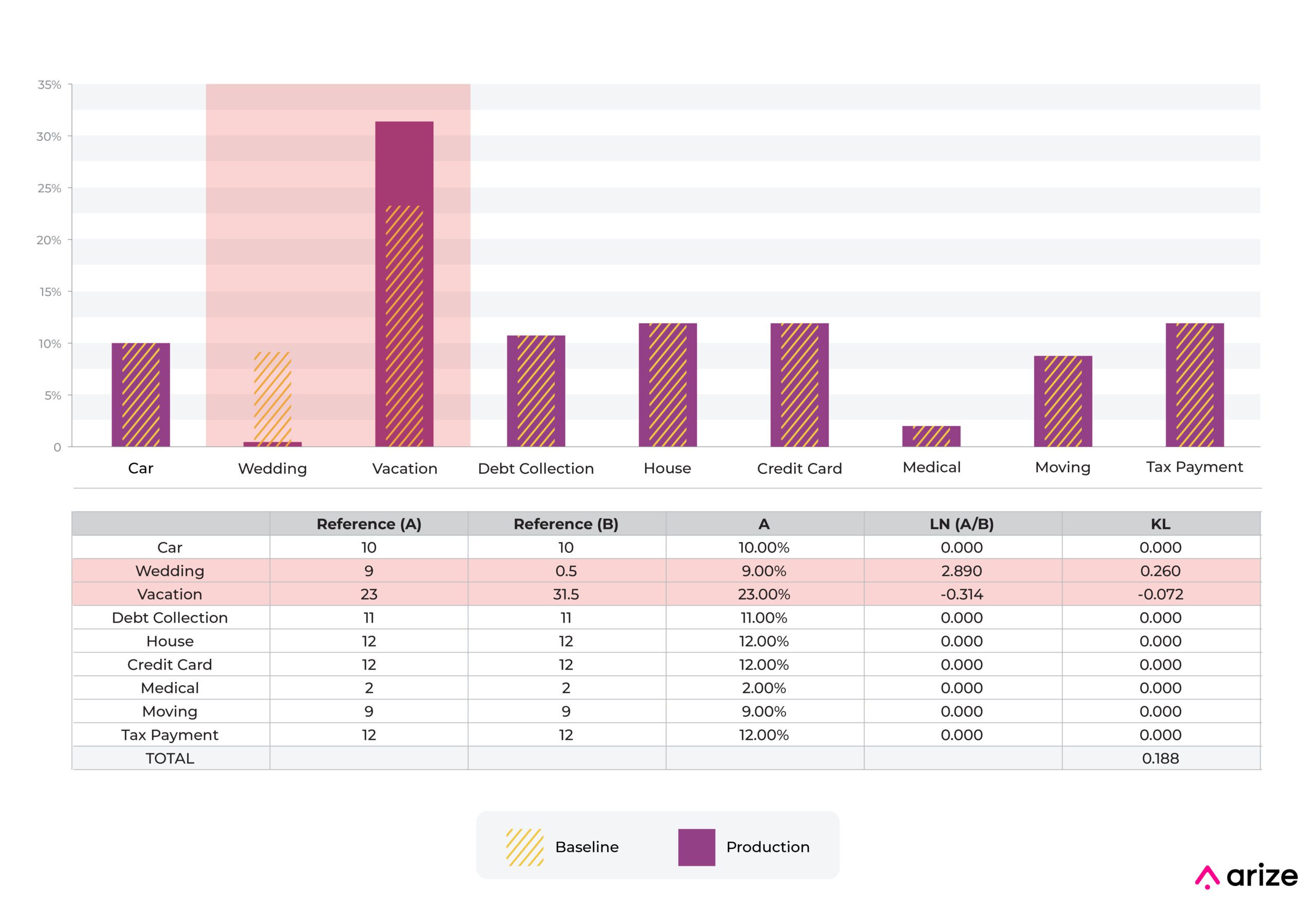
About the only way to get a large movement relative to the industry standard number of 0.2 is to move a bin down toward 0. In this example, moving a bin from 9% to 0.5% moves KL divergence a large amount.
Here is a spreadsheet for those that want to play with and modify these percentages to better understand the intuition. It’s worth noting that this intuition is very different from PSI, which will be explained in another post.
Conclusion
KL divergence is a common way to measure drift. Hopefully this practical lesson covering the intuition on the types of data movements it might catch is helpful. Additional pieces will cover binning challenges and other recommended drift metrics.